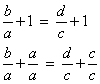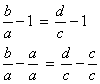Seja bem vindo!
Propriedades das proporções
1ª propriedade:
|
Numa proporção, a soma dos dois primeiros termos está para o 2º (ou 1º) termo, |
Demonstração
Considere as proporções:
 |
 |
||
|
Adicionando 1 a cada membro obtemos: |
|||
|
|
||
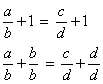Exemplo:
- Determine x e y na proporção
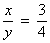, sabendo que x+y=84.
Solução:
Assim:
x+y = 84 => x = 84-y => x = 84-48 => x=36.
Logo, x=36 e y=48.
2ª propriedade:
|
Numa proporção, a diferença dos dois primeiros termos está para o 2º (ou 1º) termo, |
Demonstração
Considere as proporções:
|
|
||
|
Subtraindo 1 a cada membro obtemos: |
|||
|
|
||
(Mult. os 2 membros por -1)
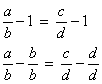Exemplo:
- Sabendo-se que x-y=18, determine x e y na proporção
.
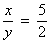Solução:
Pela 2ª propriedade temos que:
x-y = 18 => x=18+y => x = 18+12 => x=30.
Logo, x=30 e y=12.
3ª propriedade:
|
Numa proporção, a soma dos antecedentes está para a soma dos consequentes, |
Demonstração
Considere a proporção:
Permutando os meios, temos:
Aplicando a 1ª propriedade, obtemos:
Permutando os meios, finalmente obtemos:
 |
4ª propriedade:
|
Numa proporção, a diferença dos antecedentes está para a diferença dos consequentes, |
Demonstração
Considere a proporção:
Permutando os meios, temos:
Aplicando a 2ª propriedade, obtemos:
Permutando os meios, finalmente obtemos:
 |
Exemplo:
- Sabendo que a-b = -24, determine a e b na proporção
.
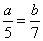Solução:
Pela 4ª propriedade, temos que:
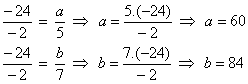
5ª propriedade:
|
Numa proporção, o produto dos antecedentes está para o produto dos consequentes, |
Demonstração
Considere a proporção:
Multiplicando os dois membros por 
, temos:
Assim:
Observação: a 5ª propriedade pode ser estendida para qualquer número de razões. Exemplo:
<< Voltar para Ensino Fundamental
Veja também: Proporção múltipla